where and when
- the tutorial has run previously as:
- - half day: "Understanding Statistics", AVI98,
L'Aquila, Italy, 1998.
- - full day: "Avoiding Damned Lies: Understanding Statistical Ideas",
CHI98, Los Angeles,
USA, 1998.
- - half day: "Understanding Statistics", HCI'96,
London, UK, 1996.
objectives
This tutorial aims develop a 'gut feeling' for several key statistical
concepts, complementing previous statistical courses by concentrating
on meaning rather than formulae.
- By the end of the tutorial you should be able to:
-
 appreciate
how random the world is appreciate
how random the world is
-
 understand
why averaging works understand
why averaging works
-
 know why
you get know why
you get 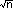 everywhere in statistics!
everywhere in statistics!
-
 interpret
significance and confidence intervals interpret
significance and confidence intervals
-
 be prepared
for the pitfalls in designing HCI and CSCW experiments be prepared
for the pitfalls in designing HCI and CSCW experiments
not an introduction
This is not an introductory statistics tutorial. It assumes that its
participants will have some experience or knowledge of statistics already.
Neither is it an advanced statistics tutorial. The range of material
it will cover will be similar to that the participants will have already
covered as part of their studies or work. The focus is on understanding
a few key concepts that make the statistics meaningful and which may
prevent serious misuse.
abstract
Many researchers and practitioners in HCI and CSCW will at
some time or another need to use or interpret experimental statistics.
However, the correct use of statistics involves a combination of mathematics
and practical know-how. Often those who have studied an introductory statistics
course have learnt how to perform the requisite mathematical manipulation,
but not the meaning of the resulting numbers. This tutorial aims to fill
the understanding gap experienced by many who use statistics, but do not
feel 'on top' of it. It will focus on the meaning of a few key concepts
and some of the common mistakes and fallacies prevalent in the HCI and
CSCW literature.
more
- Things to read:
-
 see the
tutorial outline. see the
tutorial outline.
-
 find out
about 7 common errors in statistics. find out
about 7 common errors in statistics.
-
 choose
a statistics textbook from the book list choose
a statistics textbook from the book list
- Things to play with:
-
 watch the
rain fall in Gheisra. watch the
rain fall in Gheisra.
-
 try two-horse
races with virtual coins. try two-horse
races with virtual coins.
-
 and more
coin tossing experiments. and more
coin tossing experiments.
-
 download
a HyperCard demo (stuffed binhex) download
a HyperCard demo (stuffed binhex)
- The tutorial home page is at:
- http://www.hiraeth.com/alan/tutorials/stats/
At odd times I'll add other things I think of about statistics in
HCI and CSCW . . .
. . . tell
me what you'd like to know!

|
 |

|